home

about me

work

games

other stuff

module formats

voronoi

haskell

statistics

module formats

Menu

module formats

Module Formats - Introduction

This series of posts aims to explain module music files (mods for short), how they work and how to parse and play them. We will be looking at four of the most popular file formats, the original ProTracker MOD files, the ScreamTracker 3 S3M format, the FastTracker II XM format and the IT files used by ImpulseTracker.

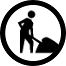
I will try to provide enough information so that someone with minimal knowledge of trackers and mod files can implement an accurate and compatible module player relatively easily and without major pain. While there is a lot of detailed information out there, much of it is incomplete, inconsistent or assumes extensive background knowledge. I will provide lists of relevant sources at the end of each post to make it easier to look thing up as needed. I will also occasionally give some background information or context that goes beyond the minimum needed to play modules. And I will make some subjective comments, which you are encouraged to disregard.

This information is intended for people who really want to implement a mod player or a tracker for whatever reason. Please remember that

• you don’t have to write your own player just to listen to modules – lots of players and converters are available, including online ones;
• you don’t need to write a library to have module music in your project – many implementations exist, including the excellent [LIB] libopenmpt library that plays any module file you have ever heard of.

If you notice that I’m missing something important or that I got something wrong, please send me a message.

History

In the 1980s, home computers were increasingly used to make music. A big revolution was the introduction of the MIDI standard, which enabled computers to control music synthesizers by sending them instructions on what to play and how. When saved to a MIDI file, these instructions are the digital equivalent of sheet music.

Even though computers had become a great tool for creating music, before 1985 they were generally quite terrible at playing it themselves, as the audio hardware built into typical home computers was rather basic and limited sound capabilities to simple chiptunes. This changed in 1985 with the introduction of the Commodore Amiga, which featured four hardware PCM channels, enabling it to play reasonably high-quality stereo samples.

Combine this capability of playing pretty much any sound based having a sample of its waveform with the idea of MIDI-style commands controlling what to play, and you have the fundamental concept of a module file: A number of samples that can be played at different pitches are used as instruments, and a list of commands defines the notes to be played along with some details such as volume and effects.

This approach to creating music was not just one possibility of many – on the Amiga it was likely the only viable option for playing interesting music. The typical Amiga had 512kB of RAM and a floppy disk capacity of 880kB. Including a full recording of a song with a demo or a game would just not have been an option, as a minute’s worth of recorded sound would have filled up the whole memory of the computer. A few different programs for creating module files, so-called trackers, emerged on the Amiga in the late 80s. The one that ended up becoming widely popular was ProTracker.

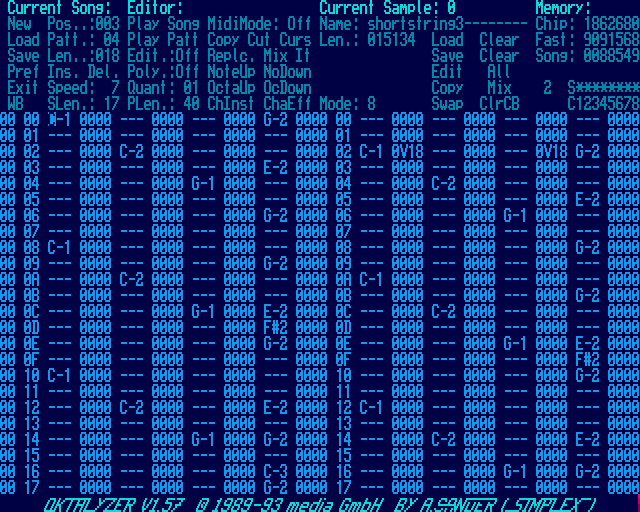
Around that time, “IBM compatible” PCs started to overcome their multimedia deficiency. VGA graphics and Adlib sound cards appeared in 1987. With the introduction and incredible success of SoundBlaster audio cards in 1989, the PC could finally almost keep up with the Amiga in terms of sound quality. As home computers were losing ground to the PC, the mod scene shifted to DOS.

ScreamTracker was one of the earlier popular trackers on the PC, and with its version 3 it introduced a module format that had a lasting impact. Following the tradition of Amiga trackers, the features of the tracker and module format mirrored functions of the underlying hardware, even including the ability to play Adlib chip sounds in a module alongside samples. The other two trackers that left an enduring legacy in the form of a popular file format were FastTracker and ImpulseTracker. These tools have in common that they were initially created in the early days of the SoundBlaster and that development ceased in the late 90s. All the popular PC trackers of the 90s were DOS programs directly tied to hardware. It seems that with the widespread adoption of Windows, their time had come.

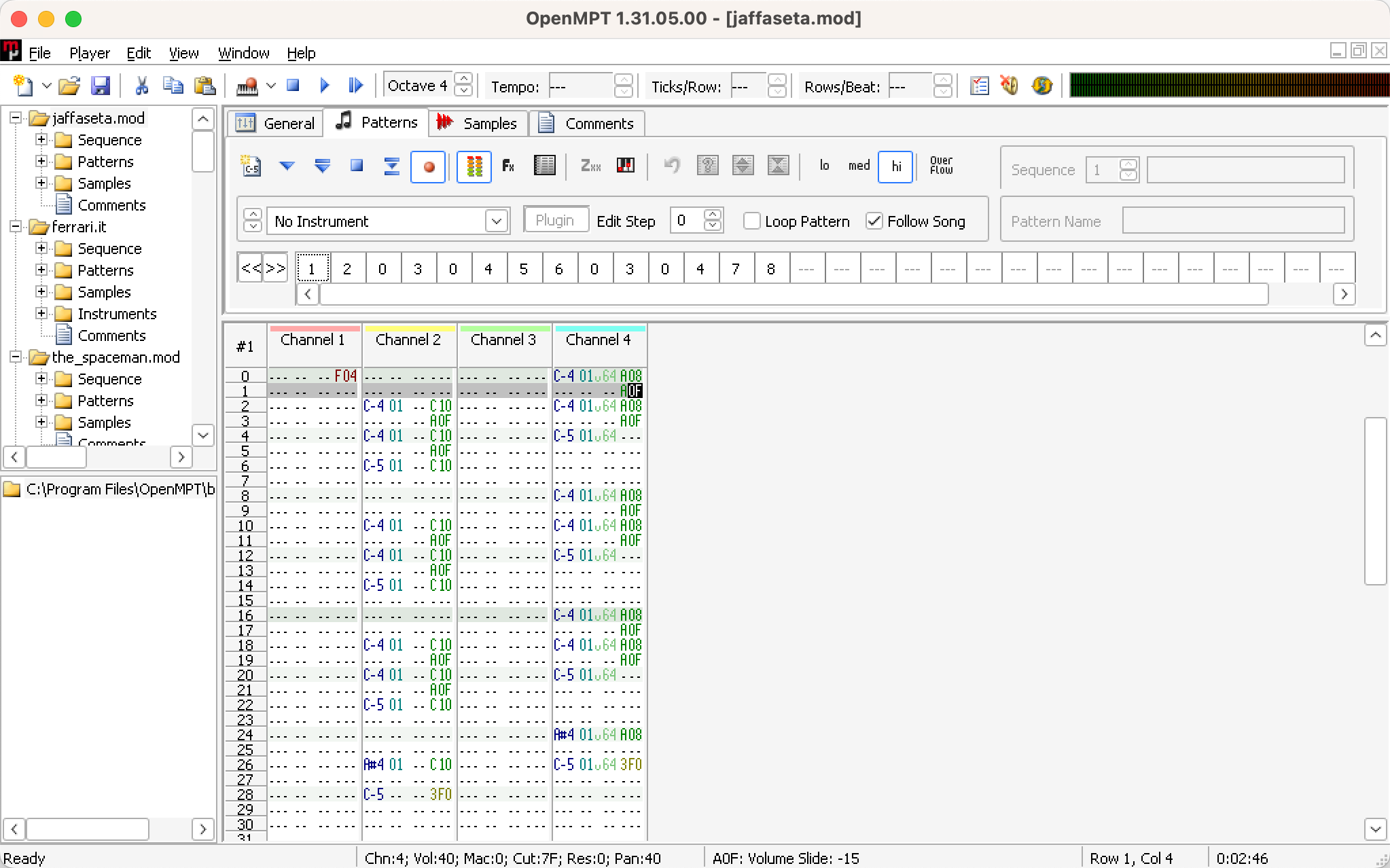
There are modern trackers that continue the legacy of the likes of ImpulseTracker. MilkyTracker is a modern recreation of FastTracker II and SchismTracker is an improved reimplementation of ImpulseTracker 2. OpenMPT combines the broad support of many formats with excellent compatibility, the ability to specifically create MOD, S3M, XM and IT files, and a modern interface. In addition to that, trackers specifically designed to create chiptune music to be played on (emulated) legacy systems such as the NES or the C64 have become a thing.

MOD File Fundamentals

The software used to create modules is called a tracker. As editors, trackers have always shown the user a very faithful and unfiltered version of the mod file. So unfiltered, in fact, that users entered much of the information such as effect commands and parameters in the form of hex numbers. This tradition is still followed today.

Because of this, looking at how the tracker represents modules gives a very accurate impression of their structure. The following picture shows ProTracker 3.1 on the Amiga.

channel row cell

The central data structure in a mod file is the so-called pattern. It is shown in the bottom half of the screen. It is a table consisting of 64 rows (sometimes called divisions – the labels are on the very left under the heading “pos”) and, in this particular case, 4 columns labelled channels #1 to #4. Each of these channels represents one largely independent sequence of notes to be played. I will refer to the intersection of a channel with a row as a cell. Every channel column is divided into 4 subcolumns (i.e. each cell contains four values; the separation is barely visible in ProTracker 3.1), representing the note to be played (e.g. B1 in channel 2, row 6), the instrument number ($07), the type of effect to be used ($0C) and a parameter for this effect ($20). Values of 0 for the instrument mean that no new instrument is being set.

Most of the effects control the volume or pitch of the playing instrument in various ways, but some affect the control flow, the playback speed or the current sample.

Clearly, channels are not tied to instruments. The instrument can be different for every note to be played in a channel, and the same instrument can be used in different channels at the same time. Channels just determine the degree of polyphony that is possible, i.e. the number of notes that can play simultaneously. The original MOD format allows for 4 channels, corresponding to four available hardware channels on the computer. Later trackers increased the number of channels, typically by using software mixing. A MOD player steps through the rows of a pattern one-by-one, playing the notes in each channel with the corresponding effects.

The time it takes to play one row the pattern is divided into a number of so-called ticks. This is a concept borrowed from the MIDI standard, where ticks correspond to the discrete points in time where commands can be issued. In MOD files, there is only one set of instructions per row, but certain effects are processed at every tick within a row. For example, an effect may reduce the volume of a channel on every tick within the current row. A typical number of ticks per row is 6.

A module can contain a large number of patterns. They do not have to be played in the order in which they are defined, however. A pattern table (also called order table) determines the order in which patterns are to be played. Patterns can show up in any order and as often as desired in this table. The maximum length of the pattern table varies by format, but is at least 128 as in MOD files. The indices of this table are called song positions. A module player typically steps through these song positions in sequence, for each playing the pattern indicated in the pattern table.

Finally, a module file contains a number of instruments. In the case of the original MOD format, an instrument is not much more that an audio sample, potentially with some information on whether we want the sample to loop. With more sophisticated formats such as XM, an instrument can include multiple samples to be used when playing different notes, information on volume envelopes and more.

A basic module player operates as follows. Its current position is given by the triple (songPos,row,tick), i.e the song position (the pattern table index, which is used to look up the current pattern), the row within the pattern at that song position and the tick number within the row. The player increments this position at the appropriate rate. While doing so, the player maintains a state for each channel which includes information on the current instrument playing (if any), its pitch and its volume. When arriving at a new row, this state is changed to reflect any new instructions provided for the channel, and then further updated at each tick as required by the effect used in this row. In the meantime, the active sample in each channel is playing continuously at the channel’s current volume and pitch.

The above description is pretty close to how a module would have been played originally. On the Amiga, each of the hardware audio channels could read samples directly from memory using DMA at a rate chosen by the program and scale them based on a provided volume value. This means that sample playback was largely automatic. The main program loop of a player thus needed to step through the MOD file, adjusting sample rates and volumes for each of the four channels at every tick as needed.

Important Concepts

Notes and Frequencies

Trackers typically allow the users to enter notes to be played by name and octave, e.g. F#3. Originally, only octaves 1 to 3 were available, although the range of possible notes has been expanded since the early days of module music. Of course, the step from one octave to the next corresponds to a doubling of the of the frequency, and each octave is divided into 12 equal relative frequency steps of \(\sqrt[12]{2}\) called semitones. Mod players cannot control the actual frequency of the sound produced by a note. All they do is scale the rate at which a sample is played. This means that playing a given instrument at A4 rather than A2 will result in four times the pitch, but whether this is anywhere near the 440 Hz we expect from an A4 depends on the sample used. The original MOD format largely imposed sample properties (a sample played at a data rate of about 8,300 Hz was supposed to be a C2), while other formats allow the user to choose the sampling rate in a more flexible way.

In order to give the composer better control over the data rates a sample is played at, some module formats make it possible to choose “finetune” values for instruments. Exact definitions vary, but the original idea is to shift the pitch by fractions of a semitone. For example, the 4-bit signed finetune parameter of a sample defined for MOD files can be used to adjust the playback rate by \(-\frac{8}{8}\) to \(+\frac{7}{8}\) of a semitone.

Periods and Data Rates

Internally, the rate at which samples are played is always represented by the sample period \(p\). When a note is triggered for an instrument, the (possibly instrument-dependent) period for the note is calculated. As long as the note keeps playing, any effects that alter the pitch will change the period in some way. This works the same, in principle, across all different module formats and format versions.

Unfortunately, things get much complicated from here on. First, the period as defined for the MOD format is not in seconds, it’s in Amiga system clock ticks. The actual data rate is \(\varphi=\frac{\Phi}{p}\), where the relevant clock rate \(\Phi\) is 3.579545 MHz on NTSC and 3.546895 MHz on PAL systems. This means that when playing a MOD file on the wrong continent, the pitch would be off by about 1%. Newer formats standardized playback rates based on the NTSC clock rate, but also scaled up the period value to allow for finer frequency adjustments.

The XM format introduces an alternative, and entirely different, way of calculating frequencies, effectively turning the “period” \(p\) into a log scale. I will discuss the details of this “linear frequency mode” in the post on the XM format.

Playback Speed

There are two numbers that affect the playback speed of a module: The number of ticks per row and the duration of a tick in seconds. There’s nothing inherently complicated about this, except that the terminology used can be confusing.

Ticks per row could be any positive integer in principle. This variable is often referred to as “speed,” even though increasing it will reduce the number of rows processed per second, everything else equal.

The length of a tick is pinned down by a value called “tempo”. It was originally thought of as beats per minute (and is sometimes referred to as BPM) of the song for a particular choice of ticks per row, see [MOD]. However, the only thing that’s important is to know that the duration of a tick is given by \(\frac{2.5\text{ s}}{\text{tempo}}\). For the default setting of 125 beats per minute, a tick thus lasts for 0.02 s.

Different documents are very inconsistent with their use of names for these two parameters. For example, [UXM] confusingly refers to ticks per row as tempo. However, all four popular mod formats use exactly the same definitions of the two “speed” parameters.

Effects

When a note is triggered on pattern row, the corresponding sample is normally played from the beginning, at the standard volume of the instrument and a constant data rate. The main role of effects is to change how the instrument is played in various ways. There are effects that modify the volume (set volume to a value, volume slides, tremolo, etc.), change the pitch (slides, vibrato, arpeggio, etc.) or affect when and how exactly the note is triggered. In addition to that, there are effects that change global parameters such as the number of ticks per row, the duration of a tick, or jump to a different point in the song.

In the MOD format, effects were given by a 4-bit effect number and an 8-bit effect parameter. Both were entered as hex numbers in the tracker. Documentations of effects will typically use a notation like 4xy or Cxx, where the first character refers to the effect number ($4=4 or $C=12), and the other two are the two nibbles of the parameter byte. For some effects, these nibbles are treated as separate parameters (4xy stands for vibrato with frequency x and depth y), in other cases they are not (Cxx means set the volume to xx). Effects that only need a 4-bit parameter are bunched together under one effect number, E in the case of the MOD and XM formats, while the first nibble of the parameter selects the actual effect. E1x stands for fine slide up by x, EDx means delay sample by x.

S3M, XM, and IT files use 8 bits to select an effect, but still follow the convention of using a single letter or number to identify an effect. XM just expands the list of effects by keeping on counting up letters beyond F, so Hxy (global volume slide) is really effect 17. S3M and IT files use the letters A to Z to refer to effects 1 through 26.

For many effects, parameter values of zero have the special meaning of “use the previous parameter.” In some cases, this is the previous parameter last used for the same effect, but in other cases different effects share their parameter memory.

While there is a large number of effects – the MOD format defines up to 31 already and other formats add to that – the good news is that for the most part, they don’t interact very much with each other beyond possibly sharing parameter memory, because only one effect can be active in each channel at a time. This is different for global effects such as jumps.

Things get more complicated with the S3M, XM and IT formats, which add a new, separate category of effects, the volume column, which will be discussed later.

Implementation Considerations

Compatibility and Generality

Is it possible or desirable to have one very general implementation of a tracker or player that can process any module file, or is it better to have different implementations for different formats? The answer to this question is a clear “it depends”.

It is certainly possible to write a program that is general enough to handle the four major module types. The IT format gets pretty close to being a superset of the features found in MOD, XM, S3M and IT, and ImpulseTracker was able to load and play files in all four formats.

Having said that, individual trackers are complex, quirky and sometimes buggy programs, and maintaining a high degree of compatibility with several of them at the same time is likely to be a hard to achieve objective. Yet, three of the four major formats are strongly tied to the tracker that introduced them, making high compatibility a desirable design objective, at least for a module player. The fourth format, MOD, is not “owned” by a single tracker in the same way as the others, but due to the technical similarities between the various Amiga trackers, many of their characteristics have become the standard for parsing MOD files.

OpenMPT maintains a high degree of compatibility by having dedicated implementations for the four big formats.

Song Characteristics

The MOD format is designed to have songs loop forever. Some module formats have facilities to mark the end of a song, but not all of them do. Some songs are intentionally designed to keep on playing in a loop, but most are not. Composers have used all kinds of tricks make it clear to a listener when a song is over. This includes inserting a gap of a few seconds before the song restarts, looping forever on an empty pattern or issuing questionable effect commands intended to halt playback.

When designing a player, it is likely desirable to detect such scenarios, determine whether a song is intended to loop or not, and if relevant detect the true end of a song.

Most modules just step through the pattern table in order, which makes it easy enough to analyse what’s happening. However, modules do have control flow commands akin to gotos and for-loops, which make things more complicated. Still, given the very limited relevant state of modules, it is not too difficult to come up with heuristics that reliably detect whether and how a song is looping, without trying to solve the halting problem.

Missing vs Empty Objects

In some of the module formats, it is possible for a module to reference an object such as a pattern or an instrument that was not present in the file. How to deal with that?

The answer is surprisingly simple. There are no missing objects, ever, just ones that were not in the file.

Trackers written in the 80s or 90s were mostly or completely developed in assembly language. There was no object orientation and little or no dynamic memory allocation. If a tracker supported n instruments, the data structures for n instruments were likely statically allocated and zero-initialized. Instruments that were not loaded were simply zero-instruments.

Therefore, if a “missing” pattern is referenced in a file, it is a default-size empty pattern. If a sample appears to be missing, the right approach may be to play a zero-length, zero-volume sample.

Somewhat related to the previous point is the issue of documented resource limits. For example, a format may have the theoretical ability to reference 256 different objects, but the documentation may insist that there is a limit of 64 or 99. These limits may be the consequence of resource constrains that are not relevant any more, or even of interface limitations. If this is plausibly the case, it may be wise not to enforce the documented limits, as newer trackers supporting the format may have relaxed them in the meantime.

Sound Quality

It is the nature of module files that samples are played at changing rates that are often but not always much lower than the resolution supported by modern audio equipment. Moreover, the samples may have a lower resolution than desirable or even compression artefacts. This tends to introduce various aliasing effects and other artefacts into the audio stream, which will typically take the form of possibly quite noticeable higher-frequency components that should not be there.

Modern trackers and players address this issue in various ways, including resampling of the instruments with interpolation techniques of varying degrees of sophistication and different filter options for audio output. While offering a range of options is probably the way to go when developing a tracker, for the purpose of just playing back legacy modules in an authentic manner, my recommendation would be to mostly go with fairly simple low-pass filters for the audio output, at least for the earlier module formats.

There is a number of reasons why I favour this approach. First, contemporary trackers and players did not use any fancy techniques to improve sound quality due to their computational costs. Second, it addresses the problem of unwanted higher-frequency noise effectively. Third, for this very reason, most audio hardware in the 80s and early 90s had built-in analogue low-pass filters that can easily be replicated digitally. Fourth, implementing first- or second-order digital filter is easy, unintrusive and computationally cheap. And finally, having the ability to filter audio output is necessary anyway for a feature-complete implementation of some module formats, although these filter-related format features are clearly not important ones.

Tabulation and Calculation

Trackers like ProTracker and ImpulseTracker tabulated functions and values, including the periods or frequencies associated with different notes. This was not primarily a matter of optimizing performance. The facilities to effectively use floating-point numbers were simply not available to these programs, so for any calculation that went beyond the scope of the basic arithmetic operations on integers, tabulation in the form of fixed-point numbers was the most practical approach.

Today, these constraints are not there anymore, and the metrics regarding the computational cost of computation versus tabulation are different. So do we still need tables?

Some tables really just contain a list of accurately rounded values that today can easily be replicated at runtime. In such cases, there is no need to clutter up sources with huge, hard-coded tables. In other cases, the numbers that were historically used don’t match the expected pattern. Some of these tables simply contain idiosyncratic oddities – they may have been made in stages over a longer time period, possibly by different people using different calculation methods (see [PTT] for an attempt to understand and explain the tables used in ProTracker). They may contain calculation errors or typos. Even in such cases, it may be desirable to just calculate the “correct” values on the fly, in particular if the numbers are not off by a significant margin.

In some situations, including pre-set tables is still be advisable. This is particularly true in situations where new module files are created and tabulated values affect either the choices a composer would make or the values written into the file. I will therefore mention the issue of tabulation occasionally when discussing particular file formats.

Whenever values are not based on externally calculated numbers, it may still be advantageous to pre-calculate them (at program start or compile time) for performance or simplicity. But in such cases, the approach to tabulation does not have to match that made by the original trackers. For example, there is no need to tabulate notes or finetune values by octave and then adjusting them by powers of two, as there are alternative options available that are both faster and more space efficient.

Some Technical Background

Volume

The volume or loudness of sound is an important property that needs to be fully understood to produce the right outcome when generating or transforming audio data. As it turns out, the term volume is not precisely defined and the underlying concept is quantified in various different ways. It’s worth taking a closer look.

When playing modules, one needs to work with samples, scaling, modulating, mixing and occasionally synthesizing them. For these purposes, the amplitude is the ideal volume measure. If we want to make sound half as loud, we just scale the samples with a factor of 0.5, reducing the amplitude to 50%. Most of the volume measures used in the context of modules have exactly this meaning, making software mixing straightforward. Technical documents such as hardware manuals occasionally use voltage to refer to the intensity of audio signals, which is proportional to amplitude.

An alternative measure of loudness is the power of sound waves. It is proportional to the square of the amplitude. Cutting the amplitude by half, everything else equal, reduces the power to 25%.

Relative volume levels are often measured on a log scale. The unit of measurement used is decibel (dB), which is defined such that 10 dB mean a ratio or factor of 10, 0 dB mean 1 and generally \(x\text{ dB}=10^{\frac{x}{10}}\). As it turns out, 3 dB is almost exactly two, and the most common use and interpretation of the decibel scale, especially when dealing with digital equipment, is to think of it as every increment of 3 dB being equivalent to a factor of 2.

By convention, it is always power-units that are measured on a decibel scale, never amplitudes. As the power is quadratic in amplitudes, doubling the amplitude means 4 times the power or a change of 6 dB. This is important to remember: every 6 dB mean a factor of 2 for the amplitude or volume of an audio signal. A reduction of the amplitude to \(\frac{1}{4}\), for example, then corresponds to a change of -12 dB.

The reduction of volume compared to a reference value, often its theoretical maximum, is referred to as attenuation. If the amplitude of a signal is lowered to \(\frac{1}{16}=2^{-4}\), it is attenuated by \(4\cdot 6\text{ dB}=24\text{ dB}\).

When parsing manuals or specification documents, it is sometimes unclear what measure “volume” refers to exactly. In software-focused documents, it usually means amplitude, unless there is a good reason to define volume differently. In the case of hardware manuals, this cannot be relied upon in general, but if well-defined terms like voltage or power are used, or if quantities are specified in volts or dB, it should be clear how to interpret them.

Filtering

Filtering audio signals is often a key aspect of audio processing, and it’s actually quite interesting. I won’t attempt to give a proper introduction to the topic here. I will instead try to explain just enough to give some intuition on why and how to filter, what filters do and how they are used. I will provide formulas for the relevant filters that can be used without having to derive anything.

Filters modify a signal by changing the amplitude or phase of its components depending on their frequencies. They do not add any components to it that were not there already.

Electronic filters for analog electric signals are important parts many types of circuits, including those dedicated to processing audio signals. They can be built out of standard components such as resistors, capacitors and inductors. The characteristics of a filter are described mathematically by its so-called transfer function, which maps frequencies to the amplitude response or “gain” of a filter. The simplest filters made up of just a few electronic components are described by transfer functions that are the quotient of two linear functions. For more complex ones with a higher number of components, the numerator and denominator of the transfer function are higher-order polynomials. The highest order of the polynomials in the transfer function is the so-called order of the filter. The coefficients of the polynomials are related to the characteristics of the underlying electronic components.

We will be interested in low-pass filters. These are filters that leave low frequencies (mostly) intact, while attenuating signal components at higher frequencies. Ideally, we might want a brick-wall filter, which eliminates all frequencies above a cut-off frequency entirely, while leaving all lower frequency components unchanged. Unfortunately, this is not possible with a finite-order filter.

While locally, filters can have all kinds of behaviour depending on the shape of the polynomials making up the transfer function, for larger frequency changes, the extent of the frequency response is limited by the order of the transfer-function polynomials. First-order low-pass filters have a so-called roll-off of 6 dB per octave, meaning that the amplitude is cut in half (-6 dB gain change) when the frequency doubles (one octave higher). This is an immediate consequence the denominator of the transfer function being linear. Second-order low-pass have a higher roll-off of 12 dB per octave, thus reducing the amplitude with the square of the frequency.

There are different types of low-pass filters one can design, which have different characteristics. The one that is of particular importance to us is the Butterworth filter, which has the desirable property of having a transfer function that is very flat for frequencies below the cut-off and generally very smooth everywhere. There are Butterworth filters of any order, although the order-one Butterworth filter is really just a generic low-pass filter. For first-order low-pass filters, the low-order polynomials making up the transfer function do not have enough coefficients to choose anything interesting but the cut-off frequency when designing the filter. We will be interested only first- and second-order Butterworth low-pass filters.

Of course, we need to filter digital signals, which are samples taken at constant intervals. Let \(x(t)\) be the unfiltered sample at time index \(t\) and \(y(t)\) the filtered sample. A digital filter of order \(n\) is simply a linear function of the \(n\) most recent unfiltered and previous filtered values:

\[y(t)=\sum_{k=0}^n b_kx(t-k)-\sum_{k=1}^n a_ky(t-k)\] The \(a\)’s and \(b\)’s are constant coefficients that determine the properties of the filter. Implementing lower-order digital filters is both simple and computationally cheap.

Now here’s the good news: There is a technique to transform any order-\(n\) analogue filter into a corresponding order-\(n\) digital filter. The resulting digital filter very accurately recreates the properties of the analogue filter at lower frequencies, but gets somewhat squished for high frequencies approaching the Nyquist frequency of \(\frac{1}{2}\) the sample rate.

I provide the coefficients for the first- and second-order Butterworth low-pass filters as a function of the desired cut-off frequency \(f_\text{cut}\) and the sample rate \(f_\text{sample}\) of the audio data to be filtered. They were calculated from the transfer function of the analogue filter using the bilinear transform with pre-warping.

Let \(W=\left(\tan(\frac{f_\text{cut}}{f_\text{sample}}\pi)\right)^{-1}\).

The coefficients for a first-order low-pass filter are:
\(b_0=b_1=\alpha\), \(a_1=(1-W)\alpha\), where \(\alpha=(1+W)^{-1}\)

The coefficients for a second-order Butterworth low-pass filter are:
\(b_0=b_2=\alpha\), \(b_1=2\alpha\), \(a_1=2(1-W^2)\alpha\), \(a_2=(1-\sqrt{2}W+W^2)\alpha\), where \(\alpha=(1+\sqrt{2}W+W^2)^{-1}\)

Don't miss that the sign of the \(a\) coefficients gets flipped in the filter formula.

References:

This is part of the OpenMPT source. The interesting thing here is the comments at the beginning of the file, containing the ProTracker finetune table and a forensic analysis of how one may have come up with these numbers.
https://resources.openmpt.org/documents/PTGenerator.c The Unofficial XM File Format Specification
https://archive.org/details/xm-file-format The MOD format documentation:
https://www.aes.id.au/modformat.html The libopenmpt library:
https://lib.openmpt.org/libopenmpt/